| |
|
| |
| 2.2 คำสั่งที่เกี่ยวข้องกับฟังก์ชันพื้นฐานทางคณิตศาสตร์ |
| ฟังก์ชันพื้นฐานทางคณิตศาสตร์ต่างๆ เช่น abs, real, imag, conj, log, exp, และ sqrt เป็นต้น ที่ใช้ในโปรแกรม SCLAB ยังคงสามารถใช้กับตัวแปรเชิงสัญลักษณ์ได้ ตัวอย่างเช่น |
-->syms a b real
-->c = a + b*%i;
-->abs(c)
ans =
sqrt(b^2+a^2) //ตัวค่าสัมบูรณ์ของ c คือ 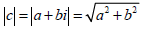
-->sqrt((a+b)^2)
ans =
abs(b+a) //เนื่องจาก 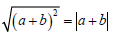
-->z = c^3
z =
(%i*b+a)^3 //เนื่องจาก 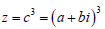
-->expand(z) //ดูรายละเอียดคำสั่ง expand ในหัวข้อที่ 2.3.1
ans =
-%i*b^3-3*a*b^2+3*%i*a^2*b+a^3 //เนื่องจาก 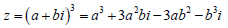
-->real(z)
ans =
a^3-3*a*b^2 //เนื่องจาก 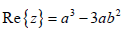
-->imag(z)
ans =
3*a^2*b-b^3 //เนื่องจาก 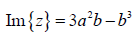
-->conj(z)
ans =
(a-%i*b)^3 |
| |
| นอกจากนี้ฟังก์ชันทางด้านตรีโกณมิติ ได้แก่ cos, acos, sin, asin, tan, และ atan ก็ยังคงสามารถใช้กับตัวแปรเชิงสัญลักษณ์ได้เช่นกัน ตัวอย่างเช่น |
-->syms a b real
-->simple(2*sin(a)*cos(a)) //ดูรายละเอียดคำสั่ง simple ในหัวข้อที่ 2.3.3
ans =
sin(2*a)
-->tan(atan(b))
ans =
b |
| |
| 2.3 คำสั่งที่เกี่ยวข้องกับพหุนาม |
| |
| 2.3.1 คำสั่ง expand |
เป็นคำสั่งที่ใช้ในการกระจายฟังก์ชันตรรกยะ (rational function) ให้อยู่ในรูปของสมการคณิตศาสตร์ โดยมีรูปแบบการเรียกใช้งานคือ |
|
| |
| เมื่อ x คือฟังก์ชันตรรกยะ และ y คือสมการคณิตศาสตร์ที่อยู่ในรูปแบบง่าย ตัวอย่างเช่น |
| |
-->syms a b c
-->x = (a + b)^2;
-->p = expand(x)
p =
b^2+2*a*b+a^2 //เนื่องจาก 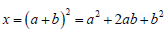
-->y = (a + b - c)^2;
-->z = expand(y)
z =
c^2-2*b*c-2*a*c+b^2+2*a*b+a^2 |
| |
| 2.3.2 คำสั่ง factor |
เป็นคำสั่งที่ใช้แยกตัวประกอบ (factorization) ของฟังก์ชันตรรกยะให้อยู่ในรูปของฟังก์ชันย่อย โดยมีรูปแบบ
การเรียกใช้งานคือ |
|
| |
| เมื่อ x คือฟังก์ชันตรรกยะ และ y คือฟังก์ชันย่อยที่ได้จากการแยกตัวประกอบ ตัวอย่างเช่น |
-->syms a b c d
-->y = (a^2 - b^2)/(c^2 - d^2); //เนื่องจาก 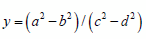
-->B = factor(y)
B =
(b-a)*(b+a)/((d-c)*(d+c)) //นั่นคือ 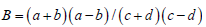
-->y = ((a+b)^2-(c+d)^2)
y =
(b+a)^2-(d+c)^2
-->B = factor(y)
B =
(-d-c+b+a)*(d+c+b+a) |
| |
| 2.3.3 คำสั่ง simple |
| เป็นคำสั่งที่ใช้ลดรูปสมการคณิตศาสตร์ให้อยู่ในรูปแบบที่ง่าย มีรูปแบบการเรียกใช้งานคือ |
| |
|
| |
เมื่อ x คือฟังก์ชันตรรกยะ และ y คือสมการคณิตศาสตร์ที่ลดรูปแล้ว ตัวอย่างเช่น |
-->syms a b
-->y = (a^2 - b^2)/(a+b);
-->B = simple(y)
B =
a-b
-->G = [cos(a) sin(a); -sin(a) cos(a)]
G =
!cos(a) sin(a) !
! !
!-sin(a) cos(a) !
-->simple(G^2)
ans =
!cos(2*a) sin(2*a) !
! !
!-sin(2*a) cos(2*a) !
-->simple(G'*G)
ans =
!1 0 !
! !
!0 1 ! |
| |
| 2.3.4 คำสั่ง numden |
เป็นคำสั่งที่ใช้เรียกดูตัวเศษและตัวส่วนของสมการคณิตศาสตร์ มีรูปแบบการเรียกใช้งานคือ |
| |
|
| |
เมื่อ Num คือตัวเศษ (numerator) และ Den คือตัวส่วน (denominator) ของสมการคณิตศาสตร์เชิงสัญลักษณ์ x ตัวอย่างเช่น |
-->syms a b
-->M = [2*a/(1+b) 0; 1 a/b];
-->[Num, Den] = numden(M)
Den =
!b+1 1 !
! !
!1 b !
Num =
!2*a 0 !
! !
!1 a ! |
| |
| 2.3.5 คำสั่ง coeffs |
เป็นคำสั่งที่ใช้เรียกดูค่าสัมประสิทธิ์ของสมการพหุนาม มีรูปแบบการเรียกใช้งานคือ |
| |
|
| |
เมื่อ c คือค่าสัมประสิทธิ์ของสมการพหุนาม A โดยที่ x คือตัวแปรของสมการพหุนามที่ต้องการหาค่าสัมประสิทธิ์และ n คือดีกรีของตัวแปร x ในสมการพหุนาม A (ค่าดีฟอลต์คือ n = 1) ตัวอย่างเช่น |
-->syms a b
-->A = (a+b)^2;
-->expand(A)
ans =
b^2+2*a*b+a^2 //เนื่องจาก 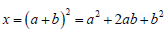
-->cof = coeffs(A, 'a', 0) //สัมประสิทธิ์หน้าตัวแปร a ที่มีดีกรีเท่ากับค่าศูนย์คือ 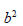
cof =
b^2
-->cof = coeffs(A, 'a', 1) //สัมประสิทธิ์หน้าตัวแปร a ที่มีดีกรีเท่ากับค่าหนึ่งคือ 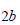
cof =
2*b
-->cof = coeffs(A, 'a', 2) //สัมประสิทธิ์หน้าตัวแปร a ที่มีดีกรีเท่ากับค่าสองคือ 1
cof =
1 |
| |
| 2.3.6 คำสั่ง degrees |
เป็นคำสั่งที่ใช้หาค่าดีกรีของตัวแปรในของสมการพหุนาม มีรูปแบบการเรียกใช้งานคือ |
| |
|
| |
เมื่อ d คือดีกรีของตัวแปร x ในของสมการพหุนาม A ตัวอย่างเช่น |
-->syms a b
-->A = (a+b)^2; //เนื่องจาก 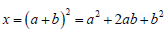
-->degrees(A, 'a')
ans =
2
-->degrees(A, 'b')
ans =
2 |
| |
| 2.3.7 คำสั่ง eval |
เป็นคำสั่งที่ใช้แทนค่า (เป็นได้ทั้งตัวเลขหรือตัวแปรเชิงสัญลักษณ์อื่นๆ) ให้กับตัวแปรเชิงสัญลักษณ์ มีรูปแบบการเรียกใช้งานคือ |
| |
|
| |
เมื่อ x คือสมการเชิงสัญลักษณ์ที่ต้องการแทนค่าตัวแปรใหม่เข้าไป ตัวอย่างเช่น |
-->syms a b c d e f
-->A = (a+b+c)^2/(d+e+f)
A =
(c+b+a)^2/(f+e+d)
-->d = a; e = b; f = c;
-->B = eval(A)
B =
c+b+a
-->a = 2; b = 3;
-->C = eval(B)
C =
c+5 |
| |
| 2.3.8 คำสั่ง dbl |
เป็นคำสั่งที่ใช้เปลี่ยนตัวเลขเชิงสัญลักษณ์ให้อยู่ในรูปของค่าสเกล่าร์ มีรูปแบบการเรียกใช้งานคือ |
| |
|
| |
เมื่อ x คือตัวเลขเชิงสัญลักษณ์ และ y คือค่าสเกล่าร์ ตัวอย่างเช่น |
-->syms x
-->y = log(x)
y =
log(x)
-->x = 4;
-->z = eval(y)
z =
log(4) //เป็นผลลัพธ์ที่อยู่ในรูปของตัวแปรเชิงสัญลักษณ์
-->dbl(z)
ans =
1.3862944 //เปลี่ยนค่า log(4) ในรูปของตัวแปรเชิงสัญลักษณ์ ให้เป็นค่าสเกล่าร์ |
| |
| |
| ก่อนหน้า [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] หน้าถัดไป |
|
|
|
|
|
|
|
| กลับด้านบน |

