5. การแยกตัวประกอบของพหุนาม
| การแยกตัวประกอบของพหุนาม (polynomial factorization) คือ การเขียนพหุนามให้อยู่ในรูปการคูณของพหุนามที่มีดีกรี |
ต่ำกว่า ตัวอย่างเช่น พหุนาม 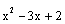 สามารถที่จะแยกตัวประกอบได้เป็น สามารถที่จะแยกตัวประกอบได้เป็น 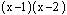 นั่นคือ นั่นคือ 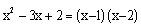 |
| ในโปรแกรม SCILAB การแยกตัว ประกอบของพหุนามสามารถทำได้โดยใช้คำสั่ง factors ซึ่งมีรูปแบบการใช้งานดังนี้ |
โดยที่ y คือสมการพหุนามที่เป็นฟังก์ชันของตัวแปรเพียงตัวแปรเดียว , g คือเลขจำนวนจริง , และ F คือเวกเตอร์พหุนาม (ที่มีดีกรีหนึ่งหรือสองเท่านั้น) ถ้ากำหนดให้ F = [f 1 f 2 f 3
f N ] เมื่อ f i คือพหุนาม ดังนั้นผลลัพธ์ที่ได้จากการใช้คำสั่ง factors คือ
ตัวอย่างเช่น
-->x = poly(0, 'x');
-->y = x^2 - 3*x + 2
y =
2 - 3x + x2
-->[F, g] = factors(y) // ผลลัพธ์ที่ได้คือ 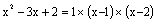
g =
1.
F =
F(1)
- 1 + x
F(2)
- 2 + x
-->F = polfact(y) // มีผลลัพธ์เทียบเท่ากับการใช้คำสั่ง factors
F =
1 - 2 + x - 1 + x
จะเห็นได้ว่าคำสั่ง polfact สามารถทำหน้าที่ในการแยกตัวประกอบของพหุนามได้เช่นเดียวกับคำสั่ง factors แต่มีรูปแบบการเรียกใช้งานต่างกันเล็กน้อย นั่นคือ
เมื่อ P = [p 0 p 1 p 2
p N ] คือเวกเตอร์พหุนาม (ที่มีดีกรีหนึ่งหรือสองเท่านั้น) และ p 0 เป็นค่าคงตัว (constant) โดยผลลัพธ์ที่ได้จากการใช้คำสั่ง polfact คือ
ตัวอย่างเช่น
-->x = poly(0, 'x');
-->y = 3*x^2 - 9*x + 6;
-->[F, g] = factors(y)
g =
3. // ผลลัพธ์ที่ได้คือ 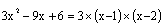
F =
F(1)
- 1 + x
F(2)
- 2 + x
-->P = polfact(y) // มีผลลัพธ์เทียบเท่ากับการใช้คำสั่ง factors
P =
3 - 2 + x - 1 + x
ในกรณีที่ต้องการแยกตัวประกอบของพหุนามที่อยู่ในรูปของเศษส่วน (rational polynomial) ก็สามารถทำได้โดยใช้ รูปแบบการเรียกใช้งานคำสั่ง factors ดังนี้
เมื่อ Q คือสมการพหุนามที่อยู่ในรูปของเศษส่วน , g คือเลขจำนวนจริง , และ N คือเวกเตอร์พหุนาม ของตัวเศษ (numerator) , และ D คือเวกเตอร์พหุนามของตัวส่วน (denominator) ในทำนองเดียวกัน ถ้าให้ N = [n 1 n 2 n 3
n k ] และ D = [d 1 d 2 d 3
d m ] เมื่อ n i และ d j คือพหุนาม (ที่มีดีกรีหนึ่งหรือสองเท่านั้น) ดังนั้นผลลัพธ์ที่ได้จากการใช้คำสั่ง factors ในกรณีนี้คือ
ตัวอย่างเช่น
-->x = poly(0, 'x');
-->Q = (3 *x^2 - 9*x + 6)/(x^2 + 3*x + 2)
Q =
6 - 9x + 3x2
--------------
2 + 3x + x2
-->[N, D, g] = factors(Q)
g =
3.
| D = // ผลลัพธ์ที่ได้คือ |
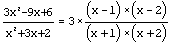 |
D(1)
1 + x
D(2)
2 + x
N =
N(1)
- 1 + x
N(2)
- 2 + x
|

