การวาดกราฟสองมิติ
คำสั่งพื้นฐานสำหรับการวาดกราฟสองมิติบนระบบพิกัดฉาก x-y คือคำสั่ง plot ซึ่งมีรูปแบบการเรียกใช้งานดังนี้
เมื่อเวกเตอร์ x เป็นตัวแปรอิสระที่กำหนดค่าในเส้นแกน x และเวกเตอร์ y ซึ่งเป็นตัวแปรตามที่กำหนดค่าในเส้นแกน y (โดยที่เวกเตอร์ y จะต้องมีขนาดเท่ากันกับเวกเตอร์ x เสมอ) นอกจากนี้คำสั่ง plot ยังสามารถที่จะถูกเรียกใช้งานได้ใน อีกรูปแบบหนึ่งคือ
ซึ่งในกรณีนี้โปรแกรม SCILAB จะสมมติว่าพารามิเตอร์ x มีค่าเท่ากับค่า 1 ถึงจำนวนสมาชิกทั้งหมดของเวกเตอร์ y นั่นคือ
x = 1:length(y) โดยอัตโนมัติ
ตัวอย่าง จงวาดกราฟของรูปสัญญาณไซนูซอยด์ (sinusoid waveform) ตามสมการ y = sin(2 ft) สำหรับเวลาที่ t = 0 ถึง 2 วินาที ถ้ากำหนดให้ความถี่ f = 1 เฮิตร์ซ (Hertz) ft) สำหรับเวลาที่ t = 0 ถึง 2 วินาที ถ้ากำหนดให้ความถี่ f = 1 เฮิตร์ซ (Hertz)
วิธีทำ จากโจทย์สามารถเขียนเป็นชุดคำสั่งของโปรแกรม SCILAB ได้ดังนี้
-->t = 0:0.01:2;
-->f = 1;
-->y = sin(2*%pi*f*t);
-->plot(t, y)
-->xtitle('A sinusoidal wave','Time (t)','Amplitude')
คำสั่งแรกเป็นการกำหนดให้ตัวแปร t ให้มีค่าอยู่ระหว่าง 0 ถึง 2 โดยที่สมาชิกแต่ละตัวที่อยู่ติดกันจะมีค่าห่างกันคงที่เท่ากับ 0.01 (ขนาดของตัวแปร t คือ 1 x 201 ) จากนั้นก็กำหนดค่าความถี่ f ให้เท่ากับหนึ่ง แล้วก็หาค่าของสัญญาณ y โดยค่า y ที่หามาได้จะมีขนาดเท่ากับตัวแปร t จากนั้นก็สั่งให้วาดกราฟขึ้นมาซึ่งผลลัพธ์ที่ได้จะเป็นกราฟตามรูปที่ 8.1 ส่วนคำสั่ง xtitle เป็นคำสั่งที่ใช้ในการ กำหนดชื่อของกราฟ , ชื่อของเส้นแกน x , และชื่อของเส้นแกน y
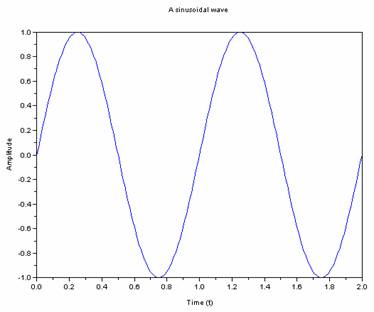
รูปที่ 8.1 สัญญาณไซนูซอยด์ y = sin(2 ft) ft)
คำสั่งวาดกราฟสองมิติอีกรูปแบบหนึ่งที่น่าสนใจก็คือ
plot2di([x], y, [options]) |
ซึ่งมีทั้งหมด 4 รูปแบบตามที่กำหนดโดยค่าพารามิเตอร์ i ดังนี้
• ไม่มี i วาดกราฟเชิงเส้นโดยใช้สเกลแบบธรรมดาหรือสเกลแบบลอการิทึม
(logarithm scale)
• i = 2 วาดกราฟขั้นบันได (step function)
• i = 3 วาดกราฟแท่ง (vertical bar)
• i = 4 วาดกราฟเชิงเส้นโดยใช้ลูกศร (arrow) แสดงทิศทางของเส้นโค้ง (curve)
ตัวอย่างเช่น
-->t = (1:0.2:7)';
-->subplot(2, 2, 1);
-->plot2d(t, [1.5+0.2*sin(t) 2+cos(t)]); // รูปที่ 8.2 ด้านบนซ้าย
-->xtitle('Plot2d - Piecewise linear');
-->subplot(2, 2, 2);
-->plot2d2(t, [1.5+0.2*sin(t) 2+cos(t)]); // รูปที่ 8.2 ด้านบนขวา
-->xtitle('Plot2d2 - Piecewise constant');
-->subplot(2, 2, 3);
-->plot2d3(t, [1.5+0.2*sin(t) 2+cos(t)]) // รูปที่ 8.2 ด้านล่างซ้าย
-->xtitle('Plot2d3 - Vertical bar plot')
-->subplot(2, 2, 4);
-->plot2d4(t, [1.5+0.2*sin(t) 2+cos(t)]); // รูปที่ 8.2 ด้านล่างขวา
-->xtitle('Plot2d4 Arrow-style plot')
ซึ่งจะได้ผลลัพธ์ตามรูปที่ 8.2 จะเห็นได้ว่าชุดคำสั่งข้างต้นมีการเรียกใช้คำสั่ง subplot(m,n,i) เพื่อช่วยทำให้สามารถวาดกราฟได้หลายๆ กราฟในหน้าต่างกราฟเดียวกัน โดยคำสั่ง subplot จะทำหน้าที่ในการแบ่งหน้าต่างกราฟออกเป็นเมทริกซ์ขนาด m x n ( m แถว และ n แนวตั้ง ) สำหรับหน้าต่างกราฟย่อยแต่ละอัน โดยหน้าต่างกราฟย่อยอันที่ i (เมื่อ i = 1, 2, ..., mn ) จะเป็นหน้าต่างกราฟย่อยที่ถูกเรียกใช้งาน
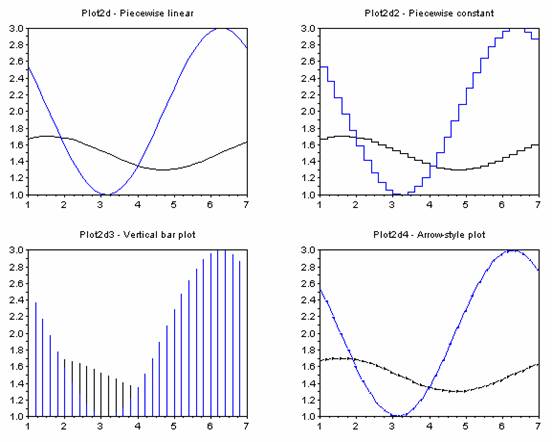
รูปที่ 8.2 ตัวอย่างรูปกราฟแบบต่างๆ ที่ได้จากการใช้คำสั่ง plot2di
พารามิเตอร์ x ในคำสั่ง plot2di คือ ตัวแปรอิสระที่กำหนดค่าในเส้นแกน x ซึ่งจะมีหรือไม่มีก็ได้ ในขณะที่พารามิเตอร์ y จะต้องอยู่ในรูปของเมทริกซ์ที่มีขนาด nc x nl เมื่อ nc คือจำนวนจุดที่จะวาดกราฟในแต่ละเส้นกราฟซึ่งจะต้องมีค่าเท่ากับจำนวนสมาชิกของพารามิเตอร์ x และ nl คือจำนวนเส้นกราฟที่จะวาด ส่วนพารามิเตอร์ options จะมีหรือไม่มีก็ได้ แต่ถ้ามีการเรียกใช้งาน options จะมีลักษณะการใช้งานดังนี้
options = [style, axesflag, leg, rect, logflag, nax, frameflag]
โดยที่
• style มีลักษณะการใช้งานคือ style = [j] โดยที่
• ถ้า j 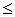 0 จะเป็นตัวกำหนดรูปแบบของเส้นกราฟที่มีรูปกากบาท วงกลม หรืออื่นๆ ปรากฎอยู่ในเส้นกราฟ 0 จะเป็นตัวกำหนดรูปแบบของเส้นกราฟที่มีรูปกากบาท วงกลม หรืออื่นๆ ปรากฎอยู่ในเส้นกราฟ
• ถ้า j > 0 จะเป็นตัวกำหนดสีของเส้นกราฟ
• axesflag มีลักษณะการใช้งานคือ axesflag = [j] โดยที่ค่าของพารามิเตอร์ j จะเป็นตัวกำหนดลักษณะของเส้นแกนในหน้าต่างกราฟ
• leg ใช้ในการใส่ข้อความบรรยาย (description) เส้นกราฟแต่ละเส้น ซึ่งมีลักษณะการใช้งาน คือ leg = "description 1 @description 2 @ ..." โดยที่ข้อความที่อยู่ภายในเครื่องหมาย "..." จะใช้บรรยายเส้นกราฟแต่ละเส้น และข้อความบรรยายเส้นกราฟแต่ละเส้นจะถูกคั่นด้วยเครื่องหมาย @
• rect ใช้กำหนดขนาดของกรอบรูปภาพซึ่งมีลักษณะการใช้งาน คือ rect = [xmin, ymin, xmax, ymax] โดยที่ xmin และ xmax ใช้กำหนดค่าต่ำสุดและค่าสูงสุดของเส้นแกน x ในขณะที่ ymin และ ymax ใช้กำหนดค่าต่ำสุดและค่าสูงสุดของเส้นแกน y ตามลำดับ
• logflag ใช้ในการกำหนดลักษณะของเส้นแกน x และเส้นแกน y ว่าจะให้เป็นสเกลแบบธรรมดาหรือสเกลแบบลอการิทึม (logarithm) โดยค่าที่เป็นได้ของ logflag มีทั้งหมดสี่แบบ คือ "nn" , "nl" , "ln" และ "ll" เมื่อ n หมายถึงให้ใช้สเกลแบบธรรมดา และ l หมายถึง ให้ใช้สเกลแบบลอการิทึม (พารามิเตอร์ตัวแรกจะอ้างอิงถึงเส้นแกน x และพารามิเตอร์ตัวที่สองจะอ้างถึงเส้นแกน y )
• nax จะ ถูกนำมาใช้เมื่อมีการเรียกใช้ พารามิเตอร์ axesflag = 1 โดย nax จะใช้ในการกำหนดลักษณะของป้าย (label) ของเส้นแกน x และเส้นแกน y ซึ่งมีรูปแบบการใช้งานคือ nax = [nx, Nx, ny, Ny] โดยที่ Nx และ Ny เป็นตัวเลขจำนวนเต็มบวกที่ใช้กำหนดจำนวนขีดหลัก (main tics) ที่จะปรากฎบนเส้นแกน x และเส้นแกน y ในขณะที่ nx และ ny เป็นตัวเลขจำนวนเต็มบวกที่ใช้กำหนดจำนวนขีดย่อย (subtics) ที่จะปรากฎอยู่ระหว่างขีดหลักสองขีดบนเส้นแกน x และเส้นแกน y
• frameflag ใช้ควบคุมขอบเขต (boundaries) ของเส้นแกน x และเส้นแกน y โดยมีลักษณะการใช้งาน คือ frameflag = [j] โดยที่ค่าของพารามิเตอร์ j จะเป็นตัวกำหนดลักษณะขอบเขตของเส้นแกนในหน้าต่างกราฟ
ผู้สนใจสามารถศึกษารายละเอียดวิธีการใช้งานตัวเลือกเหล่านี้ได้ใน [1]
8.1 กราฟเชิงขั้ว
โดยทั่วไปจุด (x, y) ที่แสดงถึงตำแหน่ง (location) บนรูปกราฟในระบบพิกัดฉากสามารถที่จะเปลี่ยนให้อยู่ในรูปของจุด(r, ) ในระบบพิกัดเชิงขั้วได้ โดยที่ r คือขนาด และ ) ในระบบพิกัดเชิงขั้วได้ โดยที่ r คือขนาด และ  คือมุมเรเดียน (เทียบกับแกน x ในทิศทวนเข็มนาฬิกา) โดยอาศัยกฎของตรีโกณมิติ ดังนั้นจากรูปที่ ก 8.3 จะได้ว่า คือมุมเรเดียน (เทียบกับแกน x ในทิศทวนเข็มนาฬิกา) โดยอาศัยกฎของตรีโกณมิติ ดังนั้นจากรูปที่ ก 8.3 จะได้ว่า

รูปที่ 8.3 ความสัมพันธ์ระหว่างจุด (x, y) ในระบบพิกัดฉาก และจุด (r,  ) ในระบบพิกัดเชิงขั้ว ) ในระบบพิกัดเชิงขั้ว
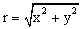 และ และ 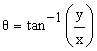
ในทำนองเดียวกันจุดพิกัด (r,  ) ในระบบพิกัดเชิงขั้วก็สามารถที่จะแปลงกลับไปเป็นจุดพิกัด (x, y) ในระบบพิกัดฉากได้จากความสัมพันธ์ดังนี้ ) ในระบบพิกัดเชิงขั้วก็สามารถที่จะแปลงกลับไปเป็นจุดพิกัด (x, y) ในระบบพิกัดฉากได้จากความสัมพันธ์ดังนี้
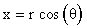 และ และ 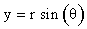
การวาดกราฟเชิงขั้วในโปรแกรม SCILAB สามารถทำได้โดยการใช้คำสั่ง
เมื่อพารามิเตอร์ theta คือค่ามุม  (มีหน่วยเป็นเรเดียน) และพารามิเตอร์ r คือค่าความยาวของรัศมี ตัวอย่างเช่น (มีหน่วยเป็นเรเดียน) และพารามิเตอร์ r คือค่าความยาวของรัศมี ตัวอย่างเช่น
-->t = 0:0.01:2*%pi;
-->polarplot(sin(7*t), cos(8*t))
ผลลัพธ์แสดงในรูปที่ 8.4
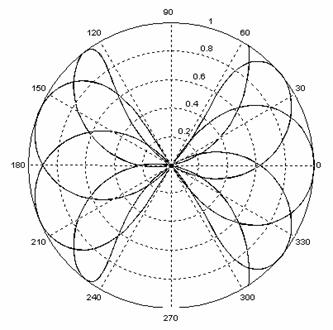
รูปที่ 8.4 ตัวอย่างรูปกราฟแสดงผลลัพธ์จากการใช้คำสั่ง polarplot
8.2 การวาดกราฟสองมิติแบบพิเศษ
นอกจากนี้โปรแกรม SCILAB ยังได้เตรียมคำสั่งสำหรับการวาดกราฟสองมิติแบบอื่นๆ ไว้ใช้งานเฉพาะด้านมากมายดังแสดงในตารางที่ 8.1 ตัวอย่างเช่น
ตารางที่ 8.1 ตัวอย่างคำสั่งในการวาดกราฟสองมิติสำหรับการใช้งานเฉพาะด้าน
คำสั่ง |
คำอธิบาย |
contour 2d |
วาดกราฟคอนทัวร์ (contour surface) จากรูปกราฟสองมิติ |
champ |
วาดกราฟสนามเวกเตอร์แบบสองมิติ (2-D vector field) |
fchamp |
วาดกราฟสนามเวกเตอร์แบบสองมิติ ที่กำหนดโดยสมการอนุพันธ์อันดับหนึ่ง (first-order ordinary differential equation) |
bode |
วาดกราฟของโบดไดอะแกรม (Bode diagram) ทั้งกราฟแสดงขนาด (magnitude plot) และกราฟแสดงมุม (phase plot)
ซึ่งมีประโยชน์มากทางด้านวิศวกรรม |
gainplot |
วาดกราฟแสดงขนาดของโบดไดอะแกรม |
nyquist |
วาดกราฟไนควิตซ์ (Nyquist plot) |
evans |
วาดกราฟอีแวนรูทโลคัส (Evans root locus) |
plzr |
วาดกราฟโพล - ซีโร่ (pole-zero plot) |
-->subplot(2, 2, 1); // รูปที่ 8.5 ด้านบนซ้าย
-->champ(-5:5, -5:5, rand(11,11), rand(11,11), ...
-->rect = [-10,-10,10,10], arfact = 2);
-->xtitle('2-D vector field plot');
-->s = poly(0, 's');
-->h = syslin('c', (s^2 + 2*0.9*10*s + 100)/(s^2 + ...
-->2*0.3*10.1*s + 102.01));
-->subplot(2, 2, 2); nyquist(h, 0.01, 100); // รูปที่ 8.5 ด้านบนขวา
-->subplot(2, 2, 3); evans(h, 100); // รูปที่ 8.5 ด้านล่างซ้าย
-->subplot(2, 2, 4); plzr(h); // รูปที่ 8.5 ด้านล่างขวา
ผลลัพธ์ที่ได้จากชุดคำสั่งนี้แสดงในรูป ที่ 8.5
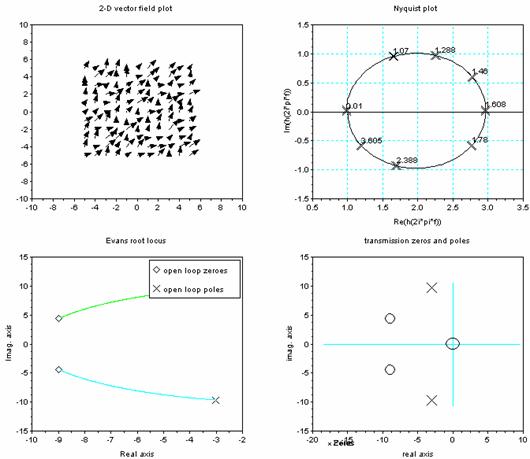
รูปที่ 8.5 ตัวอย่างรูปกราฟแสดงผลลัพธ์จากการใช้ชุดคำสั่ง สำหรับวาดกราฟสองมิติที่ใช้งานเฉพาะด้าน
|

