การดำเนินการทางคณิตศาสตร์
โปรแกรม SCILAB มีฟังก์ชันที่ใช้ในการคำนวณทางคณิตศาสตร์จำนวนมาก เช่น ฟังก์ชันพื้นฐานที่เกี่ยวกับตัวเลข , ฟังก์ชันตรีโกณมิติ , ฟังก์ชันไฮเพอร์โบลิก , ฟังก์ชันพื้นฐานทางสถิติ เป็นต้น โดยมีรายละเอียดดังต่อไปนี้
5.1 ฟังก์ชันพื้นฐาน ที่เกี่ยวกับตัวเลข ตารางที่ 5.1 แสดงฟังก์ชันพื้นฐานที่เกี่ยวกับตัวเลข ตัวอย่างเช่น
ตารางที่ 5.1 ตัวอย่างฟังก์ชันพื้นฐานที่เกี่ยวกับตัวเลข
ฟังก์ชัน |
คำอธิบาย |
abs(x) |
หาค่าสัมบูรณ์ (absolute value) ของตัวแปร x |
sqrt(x) |
หาค่ารากที่สอง (square root) ของตัวแปร x |
int(x) |
หาค่าจำนวนเต็มของตัวแปร x |
modulo(m,n) |
หาค่าเศษที่เหลือการหารตัวแปร n ด้วย m |
ceil(x) |
หาค่าจำนวนเต็มที่มีค่าใกล้กับค่า x ไปทางค่า 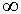 มากที่สุด มากที่สุด |
floor(x) |
หาค่าจำนวนเต็มที่มีค่าใกล้กับค่า x ไปทางค่า - 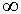 มากที่สุด มากที่สุด |
roots(p) |
หาค่ารากหรือคำตอบของสมการพหุนาม p |
real(x) |
หาค่าจำนวนจริงของตัวแปร x |
imag(x) |
หาค่าจำนวนจินตภาพของตัวแปร x |
conj(x) |
หาค่าสังยุคของจำนวนจำนวเชิงซ้อนของตัวแปร x |
exp(x) |
หาค่า e x ของตัวแปร x |
log(x) |
หาค่า log ฐาน e ของตัวแปร x |
log2(x) |
หาค่า log ฐาน 2 ของตัวแปร x |
log10(x) |
หาค่า log ฐาน 10 ของตัวแปร x |
-->abs([1, %i, -2, -2*%i, 3 + 4*%i])
ans =
1. 1. 2. 2. 5.
-->sqrt([2, 4, -1, -4])
ans =
1.4142136 2. i 2.i
-->real([0.1, %i, -1.5 + 2*%i, 2 - %i])
ans =
0.1 0. - 1.5 2.
-->imag([0.1, %i, -1.5 + 2*%i, 2 - %i])
ans =
0. 1. 2. - 1.
-->log([1, %e, 10, 20, 100])
ans =
0. 1. 2.3025851 2.9957323 4.6051702
-->log10([1, 2, 10, 20, 100])
ans =
0. 0.30103 1. 1.30103 2.
5.2 ฟังก์ชันตรีโกณมิติ โปรแกรม SCILAB ได้เตรียมคำสั่งพื้นฐานสำหรับฟังก์ชันตรีโกณมิติและฟังก์ชันตรีโกณมิติผกผัน ไว้ ตามตารางที่ 5.2 โดยค่ามุมที่ใช้หรือที่ได้รับจากฟังก์ชันทางตรีโกณมิติจะต้องมีหน่วยเป็นเรเดียน (radian) ตัวอย่างเช่น
ตารางที่ 5.2 ฟังก์ชันตรีโกณมิติและฟังก์ชันตรีโกณมิติผกผัน
ฟังก์ชัน |
คำอธิบาย |
sin(x) |
หาค่า sine ของตัวแปร x |
cos(x) |
หาค่า cosine ของตัวแปร x |
tan(x) |
หาค่า tangent ของตัวแปร x |
asin(y) |
หาค่า sine inverse ของตัวแปร y |
acos(y) |
หาค่า cosine inverse ของตัวแปร y |
atan(y) |
หาค่า tangent inverse ของตัวแปร y |
->y = sin([0, 1, %pi/2, -%pi/2])
y =
0. 0.8414710 1. - 1.
-->x = asin(y)
x =
0. 1. 1.5707963 - 1.570796 // มีหน่วยเป็นเรเดียน
-->y = tan([0, %pi/6, %pi/4, %pi/3])
y =
0. 0.5773503 1. 1.7320508
-->x = atan(y)
x =
0. 0.5235988 0.7853982 1.0471976 // มีหน่วยเป็นเรเดียน
5.3 ฟังก์ชันไฮเพอร์โบลิก
โปรแกรม SCILAB ได้เตรียมคำสั่งพื้นฐานสำหรับ ฟังก์ชันไฮเพอร์โบลิกและ ฟังก์ชันไฮเพอร์โบลิกผกผันตามตารางที่ 5.3 ตัวอย่างเช่น
ตารางที่ 5.3 ฟังก์ชันไฮเพอร์โบลิกและฟังก์ชันไฮเพอร์โบลิกผกผัน
ฟังก์ชัน |
คำอธิบาย |
sinh(x) |
ใช้หาค่า hyperbolic sine ของตัวแปร x |
cosh(x) |
ใช้หาค่า hyperbolic cosine ของตัวแปร x |
tanh(x) |
ใช้หาค่า hyperbolic tangent ของตัวแปร x |
asinh(y) |
ใช้หาค่า hyperbolic sine inverse ของตัวแปร y |
acosh(y) |
ใช้หาค่า hyperbolic cosine inverse ของตัวแปร y |
atanh(y) |
ใช้หาค่า hyperbolic tangent inverse ของตัวแปร y |
-->y = cosh([0, 1, -1])
y =
1. 1.5430806 1.5430806
-->x = acosh(y)
x =
0. 1. 1.
-->y = tanh([0, 1, -1])
y =
0. 0.7615942 - 0.7615942
-->x = atanh(y)
x =
0. 1. - 1.
5.4 ฟังก์ชันพื้นฐานทางสถิติ
โปรแกรม SCILAB ได้เตรียมฟังก์ชันสำหรับการใช้งานทางด้านสถิติ ตามที่แสดงในตารางที่ 5.4 ตัวอย่างเช่น
-->x = [3 1 4 9 2 5 7 8 6];
-->[min(x), max(x), mean(x), median(x), sum(x)]
ans =
1. 9. 5. 5. 45.
-->sort(x)
ans =
9. 8. 7. 6. 5. 4. 3. 2. 1.
ตารางที่ 5.4 ตัวอย่างฟังก์ชันพื้นฐานทางสถิติ
ฟังก์ชัน |
คำอธิบาย |
min(x) |
หาค่าต่ำสุด (minimum) ของตัวเลขทั้งหมดในตัวแปร x |
max(x) |
หาค่าสูงสุด (maximum) ของตัวเลขทั้งหมดในตัวแปร x |
mean(x) |
หาค่าเฉลี่ย (mean) ของตัวเลขทั้งหมดในตัวแปร x
(ถือเป็นค่าเฉลี่ยเลขคณิต) |
median(x) |
หาค่ามัธยฐาน (median) ของตัวเลขทั้งหมดในตัวแปร x |
sum(x) |
หาค่าผลบวกของตัวเลขทั้งหมดในตัวแปร x |
prod(x) |
หาค่าผลคูณของตัวเลขทั้งหมดในตัวแปร x |
sort(x) |
เรียงลำดับตัวเลขทั้งหมดในตัวแปร x จากค่ามากไปหาค่าน้อย |
histplot(n,x) |
วาดรูปฮิสโตแกรม (histogram) ของค่าทั้งหมดในเวกเตอร์ x เป็นจำนวน n
ช่วงระหว่างค่าต่ำสุดและค่าสูงสุดของเวกเตอร์ x |
variance(x) |
หาค่าความแปรปรวน (variance) ของตัวเลขทั้งหมดในตัวแปร x |
geomean(x) |
หาค่าเฉลี่ยเรขา (geometric mean) ของตัวเลขทั้งหมดในตัวแปร x |
ในการใช้งานทางด้านสถิติ คำสั่งที่ใช้บ่อยครั้ง คือ คำสั่ง histplot(n,x) ซึ่งเป็นคำสั่งที่ใช้ในการวาดรูปฮิสโตแกรม (histogram) ของค่าทั้งหมดในเวกเตอร์ x เป็นจำนวน n ช่วงระหว่างค่าต่ำสุดและค่าสูงสุดของเวกเตอร์ x ตัวอย่างเช่น
-->d = rand(1, 10000, 'normal');
-->subplot(1,2,1); histplot(10, d); // รูปที่ ก .1 ด้านซ้าย
-->subplot(1,2,2); histplot(20, d); // รูปที่ ก .1 ด้านขวา
คำสั่งแรกจะทำการสร้างจำนวนสุ่ม (random number) จำนวน 10000 ตัว (บรรจุไว้ในเวกเตอร์ขนาด 1 x 10000 ) โดยมีลักษณะการแจกแจงปรกติ (normal distribution) หรือการแจกแจงแบบเกาส์เซียน (Gaussian distribution) นั่นคือมีค่าเฉลี่ย (mean) เท่ากับค่า 0 และมีค่าความแปรปรวน (variance) เท่ากับค่า 1 จากนั้นก็ทำการวาดรูปฮิสโตแกรมของจำนวนสุ่มทั้งหมดโดยแบ่งข้อมูลเป็น 10 ช่วง (รูปที่ 5.1 ด้านซ้าย) และแบ่งข้อมูลเป็น 20 ช่วง (รูปที่ 5.1 ด้านขวา)
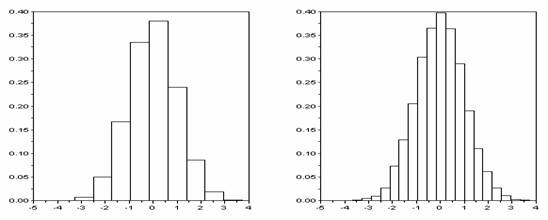
รูปที่ 5.1 ตัวอย่างรูปฮิสโตแกรม
|

