| |
3. การแก้สมการพหุนามที่มีตัวแปรเดียว
สมการพหุนาม (polynomial equation ) ที่มีตัวแปรเดียวหมายถึงสมการที่อยู่ในรูป
เมื่อ 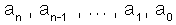 เป็นค่าคงตัว x เป็นตัวแปร และ n เป็นจำนวนเต็มบวกหรือศูนย์ เป็นค่าคงตัว x เป็นตัวแปร และ n เป็นจำนวนเต็มบวกหรือศูนย์
ถ้า 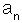 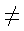 0 จะเรียกสมการพหุนามนี้ว่า สมการพหุนามดีกรี (degree) n ตัวอย่างเช่น 0 จะเรียกสมการพหุนามนี้ว่า สมการพหุนามดีกรี (degree) n ตัวอย่างเช่น
| • 2x +1 = 0 |
เป็นสมการพหุนามดีกรี 1 |
• 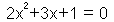 |
เป็นสมการพหุนามดีกรี 2 |
• 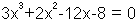 |
เป็นสมการพหุนามดีกรี 3 |
ทบทวนการแก้สมการพหุนามอย่างง่าย
สามารถแยกตัวประกอบอย่างง่ายๆ ได้ เช่น ทำให้อยู่ในรูปผลต่างของกำลังสอง ผลบวกของกำลังสาม หรือ ผลต่างของกำลังสาม อันได้แก่สูตร
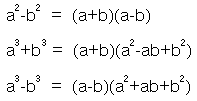
ตัวอย่างต่อไปนี้เป็นตัวอย่างการแก้สมการพหุนามอย่างง่าย
ตัวอย่างที่ 1. จงแก้สมการ 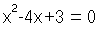
วิธีทำ
(x-1)(x-3) = 0
x-1 = 0 หรือ x-3 = 0
นั่นคือ x=1 หรือ x=3
คำตอบของสมการคือ x = {1,3} |
| |
การหาคำตอบของสมการโดยใช้โปรแกรม Scilab
-->x = poly(0,'x');
-->s = x^2 - 4*x + 3
s =
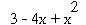
-->roots(s) // คำสั่งที่ใช้ในการหารากของคำตอบของสมการ
ans =
1.
3.
|
|
|
ตัวอย่างที่ 2. จงแก้สมการ 4x2-2x-3 =0 โดยใช้สูตร ถ้ากำหนด 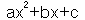 = 0 a = 0 a 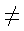 0 0 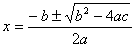
| วิธีทำ |
a = 4 , b = -2 , c = -3 |
| แทนค่า |
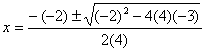 |
| |
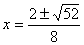 |
| |
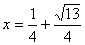 หรือ หรือ 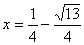 |
คำตอบของสมการคือ x = { 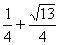 , , 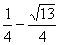 } } |
|
| |
-->x = poly(0,'x');
-->s =4*x^2 - 2*x - 3
s =
- 3 - 2x + 4x2
-->roots(s)
ans =
- 0.6513878 // ประมาณ 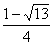
1.1513878 // ประมาณ 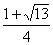
|
|
|
ตัวอย่างที่ 3. จงแก้สมการ 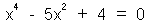
| วิธีทำ |
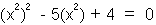 |
| และใช้วิธีการแยกตัวประกอบ จะได้ |
| |
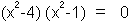 |
| (x+2) (x-2) (x+1) (x-1) = 0 |
| ดังนั้น x+2 = 0 หรือ x-2 = 0 หรือ x+1 = 0 หรือ x -1 = 0 |
| นั่นคือ x = -2 หรือ x = 2 หรือ x = -1 หรือ x = 1 |
| คำตอบของสมการคือ x = {-2 ,2 , -1 ,1} |
|
| |
-->x = poly(0,'x');
-->s =x^4 - 5*x^2 + 4
s =
4 - 5x2 + x4
-->roots(s)
ans =
1.
- 1.
- 2.
2. |
|
|
|
|

